Identidades trigonométricas
IDENTIDADES TRIGONOMETRICAS
Una identidad trigonométrica es una igualdad que vincula dos funciones trigonométricas y es válida en el dominio común o descartando los puntos que anulan alguna función en caso de ser divisor. Las funciones están ligadas por operaciones racionales y por potencias de exponente entero, aunque en algunos casos se recurre a la raíz cuadrada. Los ángulos se suman algebraicamente, se multiplican o se dividen por enteros positivos y luego actúan como argumento de alguna función.
Analicemos una de las identidades principales:
Lista de identidades trigonométricas
Hay varias identidades en trigonometría que se utilizan para resolver muchos problemas trigonométricos. Usando estas identidades o fórmulas trigonométricas, las preguntas trigonométricas complejas se pueden resolver rápidamente. Veamos todas las identidades trigonométricas fundamentales aquí.
- Identidades Pitagóricas: Hay tres identidades trigonométricas pitagóricas en trigonometría que se basan en el teorema del triángulo rectángulo o teorema de Pitágoras.
- sin2 a + cos2 a = 1
- 1+tan2 a = sec2 a
- cosec2 a = 1 + cot2 a
- Identidades reciprocas:
- Sin θ = 1/Csc θ or Csc θ = 1/Sin θ
- Cos θ = 1/Sec θ or Sec θ = 1/Cos θ
- Tan θ = 1/Cot θ or Cot θ = 1/Tan θ
- Identidades de ángulos complementarios: En geometría, dos ángulos son complementarios si su suma es igual a 90 grados. Del mismo modo, cuando podemos aprender aquí las identidades trigonométricas de los ángulos complementarios.
- Sin (90 – θ) = Cos θ
- Cos (90 – θ) = Sin θ
- Tan (90 – θ) = Cot θ
- Cot ( 90 – θ) = Tan θ
- Sec (90 – θ) = Csc θ
- Csc (90 – θ) = Sec θ
- Identidades de ángulos suplementarios: Dos ángulos son suplementarios si su suma es igual a 180 grados. De manera similar, cuando podemos aprender aquí las identidades trigonométricas de los ángulos suplementarios.
- sin (180°- θ) = sinθ
- cos (180°- θ) = -cos θ
- cosec (180°- θ) = cosec θ
- sec (180°- θ)= -sec θ
- tan (180°- θ) = -tan θ
- cot (180°- θ) = -cot θ
- Identidades de suma y diferencia de ángulos: Considere dos ángulos, α y β, las identidades trigonométricas de suma y diferencia son las siguientes:
- Identidades de ángulos duplicados: Si los ángulos se duplican, entonces las identidades trigonométricas para seno, coseno y tangente son:
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ – sin2 θ = 2 cos2θ – 1 = 1 – 2sin2 θ
- tan 2θ = (2tanθ)/(1 – tan2θ)
- Identidades de mitades de ángulos: Si los ángulos se reducen a la mitad, entonces las identidades trigonométricas para seno, coseno y tangente son
- sin (θ/2) = ±√[(1 – cosθ)/2]
- cos (θ/2) = ±√(1 + cosθ)/2
- tan (θ/2) = ±√[(1 – cosθ)(1 + cosθ)]
- Identidades producto-suma: Las identidades trigonométricas producto-suma cambian la suma o diferencia de senos o cosenos en un producto de senos y cosenos.
- Sin A + Sin B = 2 Sin(A+B)/2 . Cos(A-B)/2
- Cos A + Cos B = 2 Cos(A+B)/2 . Cos(A-B)/2
- Sin A – Sin B = 2 Cos(A+B)/2 . Sin(A-B)/2
- Cos A – Cos B = -2 Sin(A+B)/2 . Sin(A-B)/2
De esta forma, nos damos que hay una infinidad de identidades trigonométricas, que se emplean como equivalencias para tratar de manera más simple estas funciones y lograr así un manejo más versátil en pos de la solución de ecuaciones, manejo de funciones, hallar valores, etc.
Aquí les dejo una tabla con algunas identidades trigonométricas que puede llegar a servirles como formulario

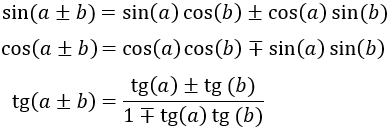
Comentarios
Publicar un comentario